Dễ dàng giải toán hình không gian với sơ đồ tư duy

Đơn giản hóa các kiến thức hình học không gian

Khi ôn tập thông qua ghi chép thông thường, sau khi ôn tập, các kiến thức bị phân tán, gây khó khăn khi xem lại. Nhưng nếu dùng sơ đồ tư duy, tất cả kiến thức liên quan và các điểm mấu chốt chỉ gói gọn trong một trang giấy.

Với quan điểm này, PGS.TS Trần Trung (Trường Cán bộ Dân tộc - UB Dân tộc Chính phủ) và thạc sĩ Đoàn Khắc Trung Ninh (Trường THPT Nguyễn Huệ - Đồng Nai) cho rằng: Trong dạy học, giáo viên có thể thay cách dạy học thông thường là giảng và viết bằng giảng và vẽ sơ đồ, đặc biệt, với các khái niệm, định lý, tính chất... có liên hệ với nhau.

Hoặc trong các bài ôn tập, thay vì dùng chữ viết để miêu tả, giáo viên có thể dùng sơ đồ tư duy giúp học sinh tiếp thu kiến thức chỉ thông qua hình ảnh hoặc các từ cần thiết. Với cách này, học sinh sẽ ghi chép nhanh chóng, dễ dàng tiếp thu và dễ ôn tập hơn.

Ví dụ, giáo viên khi ôn tập cho học sinh phần khoảng cách (lớp 11), thay vì cho học sinh ghi lại các khái niệm, tính chất, giáo viên có thể cho học sinh vẽ sơ đồ tư duy như sau:

Với sơ đồ trên, khái niệm về các loại khoảng cách trong không gian được "tối giản" và giúp làm giảm sự miêu tả của các loại khoảng cách xuống thành các hình vẽ và các từ chính.

Cách lập sơ đồ tư duy

Để giúp học sinh lập sơ đồ tư duy và dựa vào sơ đồ tư duy vừa lập để tổng hợp thành bài giải, giáo viên có thể sử dụng các câu hỏi như: 

Yếu tố nào đã cho? Yếu tố nào phải tìm? Yếu tố nào có thể duy ra hoặc tìm được? Yếu tố nào được liên hệ từ thực tiễn? Cần xuất phát từ yêu cầu nào của bài toán hay từ những điều kiện nào? Từ đây ta suy luận ra được điều gì?...

Ví dụ, cho hình chóp S.ABCD có mặt đáy là hình vuông và có cạnh bên SA vuông góc với mặt đáy. Chứng minh các mặt bên của hình chóp là các tam giác vuông.

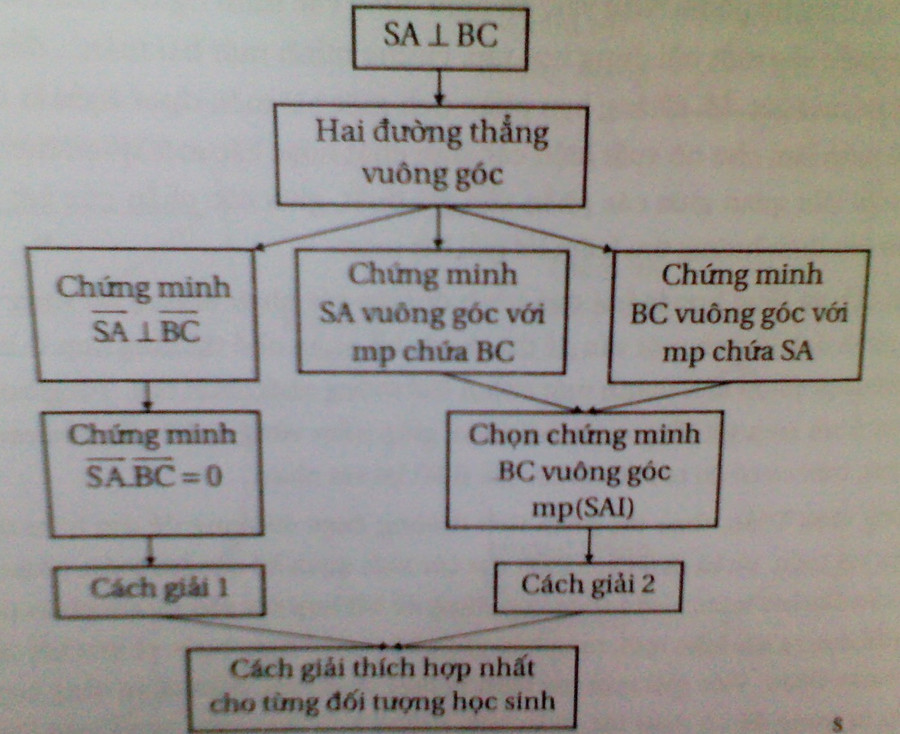
Với bài toán này, ta có 4 mặt bên gồm: mp(SAB), mp (SAD), mp(SBC), mp(SCD). Chứng minh 4 mặt phẳng này là các tam giác vuông thì quy tắc chung là chứng minh hai đường thẳng trong từng tam giác vuông góc với nhau. Vấn đề là phải chứng minh hai đường thẳng nào vuông góc với nhau?

Giáo viên có thể dùng các câu hỏi để giúp học sinh phân tích và kết hợp với sơ đồ để khái quát bài toán, từ đó tìm ra đáp án, cụ thể:

Muốn chứng minh một tam giác là tam giác vuông, ta cần chứng minh điều gì?

Để chứng minh hai đường thẳng trong không gian vuông góc với nhau, ta cần chứng minh điều gì?

Để chứng minh một đường thẳng vuông góc với một mặt phẳng ta cần chứng minh điều gì?

Giáo viên vẽ sơ đồ như sau:

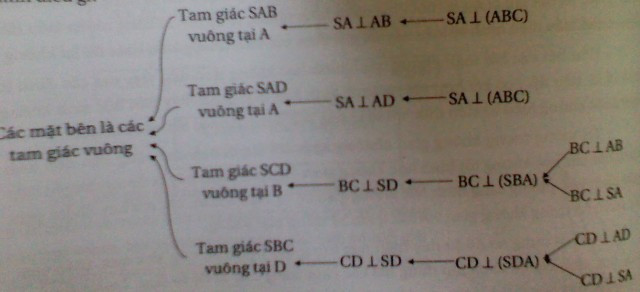Dựa vào sơ đồ trên, học sinh dễ dàng tổng hợp thành lời giải cho bài toán. Việc lập sơ đồ như trên cũng là một dạng "phân tích ngược" của bài toán, hay còn gọi là "suy ngược".

Suy ngược từ vấn đề (A) cần chứng minh, ta sử dụng những kiến thức liên quan xem là muốn có (A) thì cần có (B) và (C), muốn có (B) hoặc (C) thì lại cần có (D) và (E)... Cứ tiếp tục như vậy, ta sẽ đi đến được hướng chứng minh cho bài toán.