Hướng dẫn phát triển tư duy thuật toán cho học sinh lớp 5

Theo thầy Tô Ngọc Sơn, khi trẻ trong độ tuổi tiểu học, khả năng tư duy đã khá phát triển, trẻ đã có ý thức, ghi nhớ, tư duy tổng hợp, phân tích, phát tán và đánh giá đối với các tranh vẽ, ký hiệu, ngữ nghĩa và hành vi… Tuy nhiên, năng lực tư duy của trẻ còn bị hạn chế bởi sự ràng buộc với những thực tại vật chất cụ thể. Trẻ gặp khó khăn trong tư duy trừu tượng.

Ở lớp 5, một số nội dung chủ đề số học có thể phát triển tư duy thuật toán cho học sinh như: Cấu tạo số (số tự nhiên, phân số, hỗn số, số thập phân,…); các quy tắc thực hiện phép tính: hàng ngang, hàng dọc, quy đồng mẫu số, so sánh, quan hệ kết hợp, phân phối,…; các dạng toán có yếu tố thống kê; tìm số thập phân biết: 0,2 < x < 0,4 hay x + 3,5 = 4,72 + 2,28.

Cho biết nội dung số học và các bài tập thuộc nội dung này rất đa dạng và phong phú nhưng trong chia sẻ của thầy Tô Ngọc Sơn dưới đây chỉ giới thiệu một số dạng bài điển hình và cần thiết để minh hoạ và tham khảo.

Dạng 1: Thực hiện một dãy các phép tính

Mục tiêu dạng này nhằm giúp học sinh (HS) biết thứ tự thực hiện các phép tính; củng cố cách thực hiện cộng, trừ, nhân, chia các loại số đã học; biết cách trình bày bài tính một cách hợp lí, thuận tiện; rèn luyện và phát triển được các thao tác tư duy như quan sát – phân tích, suy luận – phán đoán, so sánh – sắp xếp, tổng hợp.

Các bước hình thành và phát triển tư duy thuật toán từng kiểu bài tập cụ thể như sau:

Kiểu bài 1: Tính giá trị biểu thức không có ngoặc đơn:

Đây là kiểu bài quen thuộc, HS đã được thao tác nhiều từ những lớp dưới, đã được giáo viên (GV) gợi mở và cung cấp các quy tắc thực hiện một cách thành thạo. Đến lớp 5 GV chỉ cần rút ra thuật toán để HS dễ nhận dạng, khắc sâu và nhớ lâu kiến thức, thực hiện một cách chuẩn xác.

Ví dụ : Tính giá trị biểu thức.

73,42 – 8,568 : 3,6 + 48,32 = 73,42 – 2,38 + 48,32

                                             = 71,04 + 48,32

                                             = 119,36

Sau khi GV tiến hành các thao tác gợi mở HS sẽ dễ dàng nhận ra các thực hiện một cách ngắn gôn và dễ nhớ, tức các em sẽ được phát triển tư duy thuật toán:

Bước 1: Tính kết quả phép chia

Bước 2: Tính kết quả phép trừ

Bước 3: Tính kết quả phép cộng.

Đối với những dạng bài tập tính giá trị một dãy các phép tính, GV cần quan sát, theo dõi từng bước tính của các em vì thường HS mắc phải sai sót là khi tính phép tính nào trước các em ghi phép tính đó ra, được kết quả rồi thêm vào những phép tính khác, sau đómới tính tiếp, hoặc các em thực hiện sai trình tự tính (sai quy tắc tính giá trị biểu thức).

Kiểu bài 2: Tính giá trị biểu thức có ngoặc đơn

Trường hợp dãy phép tính có ngoặc đơn các em thường tuân thủ theo quy tắc làm trong ngoặc trước rồi mới thực hiện các phép tính ngoài ngoặc đôi lúc làm mất thời gian và làm kéo dài các bước tính.

Ví dụ: Tính giá trị của biểu thức

[(2563 +6321) x 152 – 82497] + 487625 : 125 x 612 =

= [8884 x 152 – 82497] + 487625 : 125 x 612

= [1350368 – 82497] + 487625 : 125 x 612

= 1267871 + 487625 : 125 x 612

= 1267871 + 3901 x 612

= 1267871 + 2387412

 = 3655283

Các thao tác gợi mở giúp HS phát triển tư duy như sau:

Trong ngoặc đơn các em có thể tính được kết quả của phép tính nào trước ? (tính cộng)

Các phép tính bên ngoài dấu ngoặc các em có thể tính được kết quả của phép tính nào ? (phép chia)

Sau khi tìm được kết quả phép cộng trong ngoặc đơn có thể thực hiện tính kết quả của phép tính nào tiếp theo ? (phép nhân)

Bên ngoài ngoặc có thể thực hiện phép tính nhân không ? (được)

Như vậy, khi các phép tính trong biểu thức không ảnh hưởng lẫn nhau, không có mối quan hệ lẫn nhau thì một bước tính chúng ta có thể thực hiện như thế nào ? (Một bước có thể thực hiện cùng một lúc nhiều phép tính)

Từ các bước gợi mở trên HS có thể nêu được thuật toán như sau :

+ Bước 1 : Tính kết quả phép cộng và chia

+ Bước 2 : Tính kết quả 2 phép tính nhân

+ Bước 3 : Tính kết quả phép trừ rồi cộng số hạng bên ngoài dấu ngoặc được giá trị của biểu thức.

Như vậy biểu thức trên sẽ được trình bày gọn, nhanh, dễ hiểu.

[(2563 +6321) x 152 – 82497] + 487625 : 125 x 612 =

                                    = [8884 x 152 – 82497] + 3901 x 612

                                    = [1350368 – 82497] + 2387412

                                    = 1267871 + 2387412

                                    = 3655283

Kiểu bài 3: Tính thuận tiện nhất

Kiểu bài tính thuận tiện nhất hay tính nhanh là một trong những kiểu bài đòi hỏi HS phải biết vận dụng kiến thức đã học, biết chuyển đổi bài tính từ phức tạp thành đơn giản, có thể tính nhẫm nhanh chóng mà không cần đặt tính, từ đó nâng cao độ nhạy bén, kích thích sự sáng tạo, giúp HS phát triển tư duy rất cao.

Ví dụ : Tính bằng cách thuận tiện nhất

                                                45,28 + 52,17 – 15,28 – 12,17 =

                                                = (45,28 – 15,28) + (52,17 – 12,17)

                                                = 30 + 40

                                                = 70

Những thao tác gợi mở của GV giúp HS phát triển tư duy như sau :

Quan sát biểu thức trên các em thấy các số có dấu hiệu gì cần lưu ý? ( Có 2 cặp chữ số hàng đơn vị và phần thập phân giống nhau)

Những chữ số giống nhau nếu đem trừ nhau thì kết quả thế nào ? (bằng 0)

Vậy các em cần làm gì để tính thuận tiện hơn? (Đổi chỗ các số rồi kết hợp lại)

Khi đổi chỗ các số các em cần lưu ý điều gì? (cần đảm bảo dấu phép tính của số đó)

Như vậy để tính giá trị biểu thức một cách thuận tiện các em cần làm gì? (Cần kết hợp các số sao cho được kết quả tròn chục, tròn trăm,...)

HS phát hiện được thuật toán đối với dạng bài tính thuận tiện, tính nhanh như sau :

Bước 1: Quan sát, nhận xét biểu thức để tìm dấu hiệu đặc trưng của biểu thức liên quan đến kiến thức nào đã học

Bước 2: Chuyển đổi biểu thức, vận dụng tính chất các phép tính đã được học chuyển biểu thức đã cho về dạng đơn giản, có thể tính nhẩm thuận tiện.

Bước 3: Kiểm tra lại các bước tính và kết luận.

Dạng 2: Tìm thành phần chưa biết

Tìm x, biết  817 – x : 23 = 516

                        x : 23      = 817 – 516

                        x : 23      = 301

                        x   = 301 x 23

                        x   = 6923

Nhận xét: Trường hợp vế trái có nhiều phép tính, HS thường không xác định được tên gọi của số cần tìm nên rất dễ sai, thậm chí không tìm được kết quả, vì vậy GV cần tác động để kích hoạt tư duy các em bằng hệ thống câu hỏi gợi mở, từ đó hình thành thuật toán để khắc sâu kiến thức cho HS.

- Các bước gợi mở để phát triển tư duy cho HS:

Phép tính nào có thể thực hiện trước? (phép chia: x : 23)

Phép chia không tìm được kết quả vì chứa ẩn số x, nếu xem phép tính chia này là một ẩn số mới của phép cộng thì tên gọi của nó là gì trong phép cộng? (số hạng thứ hai)

Muốn tìm số hạng thứ hai ta làm thế nào? (lấy tổng trừ số hạng thứ nhất)

Như vậy phép chia x : 23 đã có kết quả, lúc này x có tên gọi là gì? (số bị chia)

Muốn tìm số bị chia ta làm thế nào? (lấy thương nhân với số chia)

- Đối với những bài tìm x có nhiều phép tính này GV cần khắc sâu kiến thức cho HS bằng thuật toán như sau:

Bước 1: Quan sát, nhận xét hai vế phép tính để chọn lựa và xác định thứ tự thực hiện các phép tính.

Bước 2: Xem phép tính chứa x như một ẩn số. Nếu phép tính thực hiện trước có chứa ẩn số thì xem phép tính đó như một số cần tìm, xác định tên gọi của số cần tìm này để áp dụng quy tắc tính, từng bước đưa bài toán về dạng đơn giản để tìm x.

Bước 3: Áp dụng công thức để tìm số x.

Dạng 3. Bài toán có yếu tố thống kê

Mục tiêu dạng này hiúp HS biết đọc và phân tích số liệu trên biêu đồ hình quạt; khai thác thông tin từ biểu đồ, xử lí thông tin từ biểu đồ; rèn luyện được các thao tác tư duy như suy luận – phán đoán, phân tích – tổng hợp.

Ví dụ: Kết quả điều tra về sự ưa thích các loại màu sắc của 120 học sinh được cho trên biểu đồ hình quạt bên. Hãy cho biết có bao nhiêu học sinh :

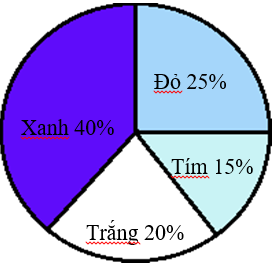a) Thích màu xanh ?

b) Thích màu đỏ ?

c) Thích màu trắng ?

d) Thích màu tím ?

Các thao tác gợi mở của GV giúp HS phát triển tư duy như sau :

Hãy đọc tên biểu đồ. (Kết quả điều tra về sự ưa thích các loại màu sắc của 120 hs)

Màu nào chiếm số phần trăm nhiều nhất ? Màu nào chiếm số phần trăm ít nhất ? (Màu xanh chiếm số phần trăm nhiều nhất, màu tím chiếm số phần trăm ít nhất)

Bài toán yêu cầu gì ? (Tìm số HS ưa thích mỗi màu)

Để tính được số HS yêu thích từng màu ta làm thế nào? (Lấy số phần trăm đã cho nhân với số HS tổng cộng đã cho rồi chia cho 100)

Vậy màu nào được HS thích nhiều nhất ? Màu nào HS thích ít nhất ? (màu xanh nhiều HS thích nhất, màu tím ít HS thích nhất)

Vậy các em có nhận xét gì về số phần trăm và số HS tương ứng vừa tính được. (Số % càng lớn thì số HS càng nhiều)

HS phát hiện và nêu được các bước thực hiện như sau :

Bước 1: Tính số HS. Áp dụng công thức tìm giá trị phần trăm của một số. (Lấy số phần trăm nhân với số HS rồi chia cho 100)

Bước 2 : Kết luận. Nêu được tên biểu đồ, số HS yêu thích màu sắc thể hiện trên biểu đồ. Nhận xét, so sánh số HS với số phần trăm đã cho.