Phương pháp “Bàn tay nặn bột” do Giáo sư Georges Charpak khởi xướng (Giải Nobel Vật lý năm 1992), được Bộ Giáo dục và Đào tạo triển khai từ năm học 2013 - 2014 chủ yếu áp dụng vào dạy học môn Tự nhiên và Xã hội (lớp 1, 2, 3) và môn Khoa học (lớp 4, 5).
“Bàn tay nặn bột” là một phương pháp dạy học tích cực, thích hợp cho việc giảng dạy các kiến thức khoa học tự nhiên. Học sinh tiểu học đang ở giai đoạn bắt đầu tìm hiểu mạnh mẽ các kiến thức khoa học, hình thành các khái niệm cơ bản, tập trung phát triển khả năng nhận thức.
Phương pháp này giúp các em tìm ra lời giải đáp cho những thắc mắc trẻ thơ bằng cách: Đặt vào tình huống có vấn đề; từ thắc mắc đến dự đoán; tự mình khám phá tìm ra lời giải. Đó cũng chính là cơ sở để thầy, cô giáo chúng ta vận dụng phương pháp “Bàn tay nặn bột” một cách sáng tạo sang dạy môn Toán.
Từ quan điểm đó, tôi xin trình bày cách vận dụng phương pháp này vào dạy bài “Diện tích hình thang” – Toán lớp 5.
Tiến trình dạy dạng bài hình thành kiến thức mới nói chung và bài “Diện tích hình thang” nói riêng gồm có 4 phần: Khởi động; Hình thành kiến thức mới; Thực hành – luyện tập; Vận dụng. Tôi chỉ áp dụng phương pháp dạy học này vào phần Hình thành kiến thức mới.
Phần chuẩn bị:
- Giáo viên: Giấy bìa cứng, giấy A3 đủ cho các nhóm làm việc.
- Học sinh: Kéo, keo dán, thước kẻ, vở ghi kết quả thực hành, 2 hình thang giống nhau bằng bìa cứng.
- Chia nhóm học sinh (cần linh hoạt, tùy vào trường hợp cụ thể có thể chia theo vị trí chỗ ngồi, theo sở thích, theo tháng sinh, hoặc theo thứ tự bảng chữ cái ABC…).
Các bước thực hiện:
Bước 1: Đưa ra tình huống xuất phát và câu hỏi nêu vấn đề.
Giáo viên đặt vấn đề bằng câu hỏi: Em đã được học cách tính diện tích các hình nào? (Hình vuông, hình chữ nhật, hình bình hành, hình thoi, hình tam giác). Tương tự như bài Diện tích hình tam giác, các em hãy tìm cách tính diện tích hình thang dựa trên cách tính các hình đã được học.
Bước 2: Bộc lộ quan niệm ban đầu của học sinh.
Dựa trên các đồ dùng đã chuẩn bị, các em hãy suy nghĩ xem chúng ta có thể tính diện tích hình thang bằng cách nào? Giáo viên khuyến khích học sinh nêu những suy nghĩ, nhận thức ban đầu của mình.
Các nhóm nêu câu trả lời: Ví dụ:
- Cắt hình thang thành hình tam giác
- Cắt hình thang thành hình chữ nhật
- ……………………..
- Giáo viên cho học sinh trình bày bằng hình thức: Viết, vẽ, nói….
Bước 3: Đề xuất câu hỏi và nêu phương án thực nghiệm.
Dự kiến những câu hỏi học sinh có thể nêu:
- Hình thang có thể cắt ghép thành hình gì? (Tùy trình độ học sinh, giáo viên có thể khéo léo gợi ý hình thang có thể cắt thành hình chữ nhật hoặc hình tam giác).
- Dựa vào yếu tố nào để tính được diện tích hình thang?
- Từ bài học này, giáo viên củng cố cách tính diện tích hình tam giác.
- Các nhóm lựa chọn hình mình cắt ghép.
Bước 4: Tiến hành thực nghiệm tìm tòi.
(Học sinh có thể thực hiện một trong các cách sau, nếu quá khó so với trình độ các em thì giáo viên có thể gợi ý).
Cách 1: Học sinh cắt ghép hình thang thành hình tam giác.
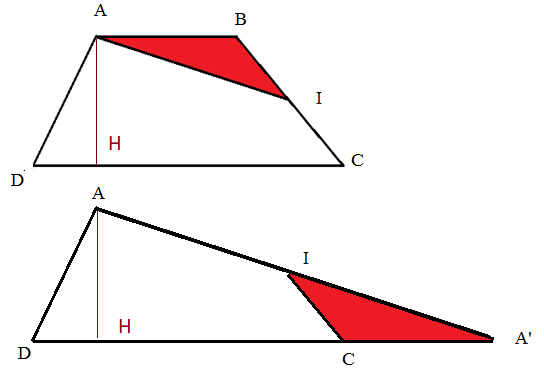
Lấy trung điểm I trên cạnh bên BC, dùng kéo cắt theo mép AI, được tam giác ABI ghép thành hình tam giác AA’D (điểm B trùng với điểm C). Hướng dẫn học sinh quan sát để nhận ra đáy DA’ của tam giác AA’D bằng tổng 2 cạnh đáy AB và CD của hình thang ABCD.
Vận dụng công thức tính diện tích hình tam giác ở bài trước, học sinh tính được S.AA’D = DA’ x AH : 2.
Từ đó các em ghi vào vở thực hành S.ABCD = (AB + CD) x AH : 2
Vậy diện tích hình thang bằng tổng 2 đáy nhân chiều cao rồi chia 2.
Cách 2: Học sinh cắt ghép hình thang thành hình chữ nhật.
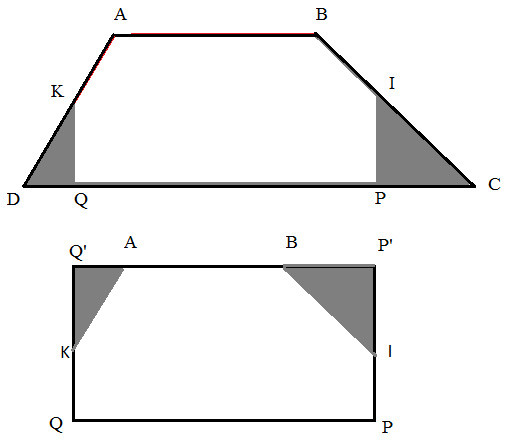
Lấy 2 trung điểm K và I của 2 cạnh bên AD và BC, qua hai trung điểm đó vẽ 2 đường thẳng vuông góc với cạnh đáy CD của hình thang. Dùng kéo cắt theo mép IP được hình tam giác IPC. Ghép tam giác IPC vào vị trí IP’B (điểm C trùng với điểm B).
Tương tự, cắt theo mép KQ được hình tam giác KQD. Ghép tam giác KQD vào vị trí KQ’A (điểm D trùng với điểm A). Sau khi cắt ghép được hình chữ nhật Q’P’PQ. Diện tích hình thang ABCD bằng diện tích hình chữ nhật Q’P’PQ.
Mà diện tích hình chữ nhật Q’P’PQ bằng chiều cao hình thang ABCD nhân với PQ (PQ chính bằng trung bình cộng 2 đáy AB và CD của hình thang ABCD).
(Giáo viên quan sát lớp, giúp đỡ để các em nhận ra chiều dài PQ của hình chữ nhật chính bằng trung bình cộng của hai đáy AB và CD để học sinh dễ dàng tính được và ghi vào vở thực hành).
SQ’P’PQ = (AB + CD) : 2 x PP’(PP’ bằng chiều cao AH của hình thang ABCD)
Nên SABCD = (AB + CD) : 2 x AH
Vậy diện tích hình thang bằng tổng 2 đáy chia 2 rồi nhân chiều cao.
Bước 5: Kết luận, khái quát hóa kiến thức mới.
Các nhóm sau khi đã thực nghiệm, tiến hành chia sẻ và trình bày trước lớp. Trong quá trình học sinh chia sẻ, giáo viên giúp các em nhận ra dấu hiệu, yếu tố để tính được diện tích hình thang.
Khái quát hóa nội dung bài học bằng quy ước: Gọi diện tích hình thang là S, 2 cạnh đáy của hình thang lần lượt là a và b, chiều cao là h. Em hãy viết công thức tính diện tích hình thang.
Học sinh viết vào vở thực hành, giáo viên chốt ý ghi bảng nội dung bài học: S = (a + b) x h : 2.
Có thể nói rằng, tổ chức các hoạt động dạy học theo những phương pháp mới là quá trình cả giáo viên và học sinh dám từ bỏ lối mòn, rập khuôn máy móc để thực hiện những điều mới mẻ vượt ra khỏi phạm vi của sách giáo khoa.
Rất khó thực hiện nhưng làm được chính là chúng ta đang thổi vào lớp học một luồng gió mới. Học sinh phấn chấn, hào hứng và tích cực hơn trong các hoạt động; các em được trực tiếp làm việc, suy nghĩ, nghiên cứu, tìm ra câu trả lời cho các vấn đề các em đặt ra, tạo ra cách thức và lối tư duy mới.
Cũng từ đó các bài toán hình học nâng cao không phải trở nên quá khó. Như vậy, dạy học toán bằng phương pháp “Bàn tay nặn bột” là một mũi tên trúng nhiều đích, các em vừa nắm được kiến thức, kĩ năng bài học, vừa phát triển được năng lực phẩm chất của con người trong thời đại mới: Luôn sẵn sàng, chủ động tìm tòi và khám phá…