Tổ chức tiếp cận bài toán phương trình đường thẳng theo nhiều cách
Để rèn luyện sự linh hoạt mềm dẻo cho học sinh trong hoạt động giải toán, cô Phan Thị Kim Ngân - Trường THPT Dương Quảng Hàm (Văn Giang, Hưng Yên) – cho rằng, trước tiên nên rèn luyện khả năng phát biểu bài toán nhiều cách khác nhau.
Khả năng này sẽ giúp học sinh không chỉ nắm vững kiến thức đã học, tìm được mối quan hệ giữa chúng, mà trên cơ sở đó sẽ tìm ra được nhiều cách giải cho bài toán, đồng thời khả năng tư duy toán học cũng được rèn luyện và phát triển.
Trên lớp, trong các giờ học, cô Ngân cho rằng, giáo viên có thể thiết kế các ví dụ như sau:
Ví dụ : Phát biểu lại bài toán bằng nhiều cách khác nhau:
"Trong mặt phẳng toạ độ (xOy) cho tam giác ABC có A(2;5); B(-1; -2); C(7;-2). Viết PT đường cao qua đỉnh A".
HS cần tự mình huy động kiến thức để tìm kiếm các lý thuyết tương đương và tìm ra cách phát biểu mới. Từ đó HS có thể tìm được một số cách phát biểu khác của yêu cầu bài toán là:
Cách 1: Viết PTĐT qua đỉnh A vuông góc với cạnh BC.
Cách 2: Viết PTĐT qua đỉnh A nhận véc tơ làm VTPT.
Cách 3: Viết PTĐT qua đỉnh A vuông góc với trục Ox.
Cách 4: Viết PTĐT qua đỉnh A song song với trục Oy.
Cách 5: Viết PTĐT đi qua đỉnh A và chân đường vuông góc của A trên cạnh BC
Cách 6: Viết PTĐT đi qua đỉnh A và trực tâm của tam giác ABC.
Cách 7: Viết PTĐT đi qua trực tâm của tam giác ABC và vuông góc với cạnh BC.
Cách 8: Viết PTĐT đi qua đỉnh A và giao điểm của hai đường trung trực của các cạnh AB, AC.
Trong giải toán nếu HS biết khai thác, phát biểu, suy luận các giả thiết theo nhiều hướng khác nhau thì sẽ dễ dàng tìm lời giải, có thể là nhiều lời giải cho bài toán.
Xem các ví dụ khác cô Phan Thị Kim Ngân chia sẻ TẠI ĐÂY
Khai thác những bài toán về đường thẳng có nhiều cách giải
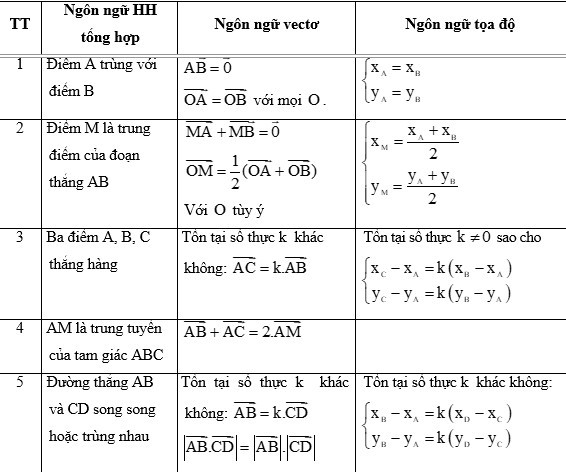
Kinh nghiệm của cô Phan Thị Kim Ngân là: khai thác những bài toán có thể hiểu theo nhiều dạng ngôn ngữ: ngôn ngữ vectơ, ngôn ngữ hình học tổng hợp, ngôn ngữ toạ độ. Chẳng hạn:
 |
 |
 |
Việc hình thành cho HS chuyển đổi ngôn ngữ các kiến thức cơ bản sẽ giúp các em dễ dàng huy động kiến thức để giải quyết vấn đề.
Ví dụ: Giải bài toán bằng nhiều cách: "Trong mặt phẳng toạ độ (xOy) cho tam giác ABC có A(1;-2), B(5;4), C(-2;0) . Viết phương trình đường phân giác trong góc A".
Giáo viên có thể cùng HSphân tích để định hướng các cách giải bài toán: Để viết phương trình đường phân giác trong của góc A, cách các em thường nghĩ tới trước tiên chính là sử dụng phương trình đường phân giác của góc tạo bởi hai đường thẳng cắt nhau, sau đó dựa vào tính chất đường phân giác trong thì cắt đoạn thẳng BC để loại bớt phương trình đường phân giác ngoài.
Cách này khá thông thường, nó thể hiện mức độ nắm vững và biết vận dụng kiến thức cơ bản, có liên quan vào việc giải toán.
Thông thường ta làm như sau:
 |
Tuy nhiên ở khả năng nhuần nhuyễn, HS có thể suy luận việc viết phương trình đường phân giác trong có thể tiến hành nhanh hơn mà không phải loại bớt các trường hợp. Đó là cách xác định chân đường phân giác hạ từ A xuống cạnh BC.
 |
Ở cấp độ cao hơn về mặt TD ta có cách giải khá độc đáo, ngắn gọn. Độc đáo ở chỗ chuyển từ hai góc bằng nhau sang tích vô hướng của các vectơ mà việc xác định nó đơn giản.
 |
Xem các ví dụ khác cô Phan Thị Kim Ngân chia sẻ Tại đây
Theo cô Phan Thị Kim Ngân, có một số lượng lớn các bài tập trong hình học phẳng và hình học vectơ có thể chuyển đổi sang ngôn ngữ tọa độ và cho lời giải gọn gàng nhanh chóng. Để HS linh hoạt hơn trong sử dụng các ngôn ngữ hình học khác nhau để giải quyết vấn đề, giáo viên nên đưa ra hệ thống các bài tập có thể giải quyết được bằng nhiều cách khác nhau.
Thiết kế, hướng dẫn và tổ chức hoạt động phát hiện bài toán mới từ bài toán cơ bản
Phát hiện bài toán mới nhờ thay đổi một số nội dung của bài toán ban đầu
Theo cô Phan Thị Kim Ngân cho rằng, mục đích phần này nhằm rèn luyện tính mềm dẻo của tư duy, linh hoạt trong tư duy của HS nhưng ở cấp độ cao hơn các biện pháp đã đề ra phía trên.
Ở cấp độ này, HS được học tập và rèn luyện các cách tiếp cận một bài toán theo hướng khai thác và phát hiện các hướng để tạo ra bài toán mới.
Cấu tạo dạng bài tập này có gồm hai phần: Phần thứ nhất là bài toán H. Phần thứ hai là bài toán H nhưng đã được biến đổi một vài yếu tố của nó.
Tác dụng của dạng bài này là rèn luyện khả năng chuyển từ hoạt động trí tuệ này sang hoạt động trí tuệ khác chống "tính ỳ" của tư duy. Vì vậy, giáo viên rất nên sử dụng dạng bài này thường xuyên trong các tiết học để giúp HS rèn luyện khả năng tiếp cận bài toán dưới nhiều cách khác nhau cũng như "khơi" gợi dần khả năng sáng tạo của các em.
Để tập luyện khả năng này, cô Phan Thị Kim Ngân chia sẻ, giáo viên có thể hướng dẫn các em hoạt động theo 3 cấp độ:
Cấp độ 1: Giáo viên làm mẫu. HS lắng nghe, ghi chép và tự phân tích.
Cấp độ 2: Giáo viên hướng dẫn HS cùng tham gia sáng tạo bằng các câu hỏi gợi ý.
Cấp độ 3: Giáo viên giao việc cho HS tự sáng tạo bài toán mới.
Việc biến đổi một vài yếu tố của bài toán ban đầu để tạo ra bài toán mới khá đa dạng. HScó thể tập thay thế một hoặc một vài giả thiết ban đầu bằng các giả thiết tương tự, hoặc có tính chất thay thế mà có tác dụng chuyển đổi hướng giải giải quyết của bài toán và giữ nguyên yêu cầu bài toán.
Cũng có thể làm ngược lại: ta giữ nguyên các giả thiết của bài toán và thay đổi yêu cầu của bài toán bằng cách thu hẹp bớt các yêu cầu, hoặc xem xét thêm với các giả thiết đã ra của bài toán còn giúp ta tìm ra thêm các kết quả nào nữa không?
Chính tư tưởng "tấn công" này sẽ tạo ra sự linh hoạt, nhạy bén trong tư duy của HS và là con đường dẫn tới sáng tạo toán học.
Trong việc mở rộng thêm yêu cầu bài toán đôi khi gặp khó khăn vì các giả thiết ban đầu của bài toán cung cấp không đủ. Khi đó ta cần xem xét bổ xung thêm giả thiết nào cho bài toán có thể giải được? Cứ như vậy ta tìm được những bài toán mới ở cấp độ phức tạp, tổng quát hơn bài toán ban đầu với nội dung đã thay đổi cả về giả thiết lẫn yêu cầu đặt ra.
Xem ví dụ cô Phan Thị Kim Ngân chia sẻ Tại đây
Phát hiện bài toán mới bằng cách tư duy thuận nghịch bài toán ban đầu
Kinh nghiệm cô Phan Thị Kim Ngân chia sẻ về nội dung này như sau:
Về mặt cấu tạo, ở dạng đơn giản nhất, bài tập dạng này gồm một cặp bài có nội dung ngược nhau (cái phải tìm của bài này trở thành cái đã cho của bài kia và ngược lại). Có một số bài toán được xuất hiện dưới dạng mệnh đề điều kiện cần và đủ và đa số các bài tập là dạng mệnh đề một chiều.
Bài toán nào cũng có mệnh đề đảo, tuy nhiên các mệnh đề đảo đó có thể đúng hoặc sai, do đó người thầy phải chuẩn bị trước và đoán nhận kết quả để hướng dẫn cho các em.
Với bài toán đảo thường khó giải hơn bài toán thuận, cho nên đòi hỏi các em phải vận dụng nhiều kiến thức hơn, tư duy sắc sảo hơn để giải quyết vấn đề, tất nhiên điều này sẽ là động cơ tạo hứng thú học tập cho các em và đặc biệt là phát triển được tư duy sáng tạo.
Với những mệnh đề đảo sai thì giáo viên hướng dẫn HS bổ sung thêm một số giả thiết hợp lý để được một mệnh đề đúng. Vậy để thiết lập bài toán mới từ mệnh đề đảo ta có thể thực hiện như sau:
Bước 1: Giải bài toán đã cho.
Bước 2: Lập mệnh đề đảo về một tính chất nào đó của bài toán, chứng minh mệnh đề đảo này để có bài toán đảo.
Bước 3: Nếu mệnh đề đảo chưa đúng thì bổ sung thêm một số giả thiết hợp lý và chứng minh để có bài toán đảo.
Bước 4: Kết luận và phát biểu bài toán đảo.
Tác dụng của loại bài tập này chính là rèn luyện tính thuận nghịch của tư duy. Đây là một trong những cách tạo ra tình huống có vấn đề, với hoạt động này các em sẽ học tập tích cực, chủ động và mềm dẻo hơn trong các hoạt động tư duy sáng tạo hơn, bởi chính các em đưa ra các bài toán đảo và tự giải các bài toán đó.
Hơn thế nữa là các em được học từ việc học: học được cách xem xét một vấn đề theo chiều xuôi, chiều ngược, học được cách tìm tòi khám phá, không muốn dừng ở những điều đã có.
Trong quá trình rèn luyện tư duy này, giáo viên cũng nên lựa chọn hệ thống bài tập có tính phân bậc từ đơn giản đến phức tạp, xuất phát từ những bài tập đơn giản trong giáo khoa để tăng thêm tính hấp dẫn thu hút được nhiều đối tượng HS.
Xem ví dụ cô Phan Thị Kim Ngân chia sẻ Tại đây
Xây dựng chuyên đề nâng cao về phương trình đường thẳng cho học sinh
Cô Phan Thị Kim Ngân nhận định: Thực tế cuộc sống hơn lúc nào hết đòi hỏi toàn ngành giáo dục phải có sự đổi mới bắt kịp với yêu cầu của đổi mới đất nước, tạo ra sản phẩm giáo dục là thế hệ mới năng động, nhạy bén, linh hoạt trong tư duy và trong cuộc sống.
Muốn như vậy, HS cần được trang bị các phương pháp tự học, phương pháp tư duy một cách mềm dẻo và sáng tạo. Bên cạnh đó, cần chú trọng phát hiện và bồi dưỡng rèn luyện tài năng của các em có năng khiếu chuyên biệt, đây chính là lực lượng nòng cốt sẽ góp phần quan trọng cho sự phát triển đất nước sau này.
Vì vậy, giáo viên cần xây dựng những chuyên đề mang tính sáng tạo nhằm góp phần bồi dưỡng rèn luyện tài năng của HS có năng khiếu chuyên biệt.
Xem các ví dụ khác cô Phan Thị Kim Ngân chia sẻ Tại đây





































