Theo thầy Mạnh Tường Vi - Phó hiệu trưởng Trường THCS Giảng Võ (Hà Nội), giải một bài toán cực trị hình học cần phải vận dụng nhiều kiến thức và kỹ năng tổng hợp, trong đó có kỹ năng chứng minh các thuộc tính hình học, có phương pháp giải toán quỹ tích, toán dựng hình, tìm điểm cố định, hình cố định, nhiều khi phải vận dụng bất đẳng thức và cực trị đại số.
Tóm lại, toán cực trị hình học hội tụ rất nhiều kiến thức, kỹ năng và phương pháp giải toán sơ cấp. Vì vậy, học sinh giải toán cực trị phải huy động và qua đó được củng cố, khắc sâu kiến thức toán rất nhiều. Đây cũng là một mảng kiến thức hay được đề cập trong các đề thi học sinh giỏi và trong các đề thi vào các trường phổ thông chuyên.
Phương pháp giải các bài toán cực trị hình học được thầy Mạnh Tường Vi chia sẻ như sau:
Phương pháp 1: Vận dụng quan hệ giữa đường xiên và đường vuông góc:
 |
Phương pháp 2: Quan hệ giữa đoạn thẳng và đường gấp khúc:
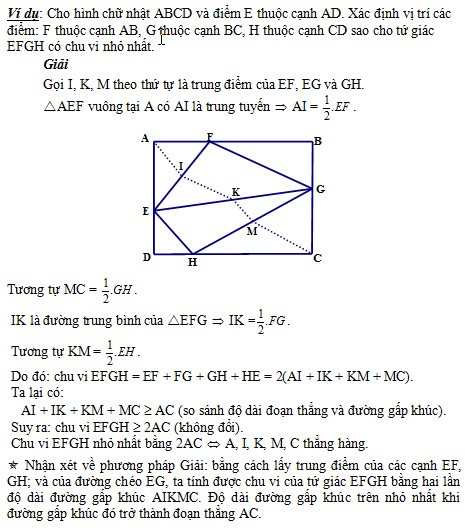 |
Phương pháp 3: Áp dụng bất đẳng thức trong tam giác và đường tròn tìm cực trị:
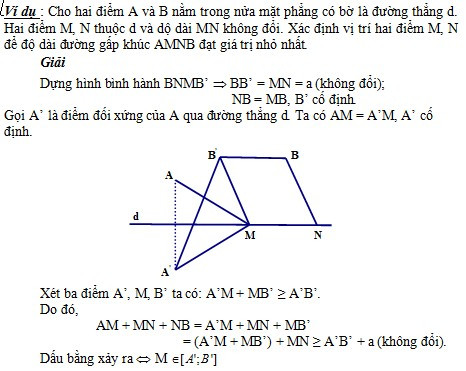 |
Phương pháp 4: Áp dụng bất đẳng thức đại số:
 |
Phương pháp 5: Ứng dụng diện tích tìm cực trị:
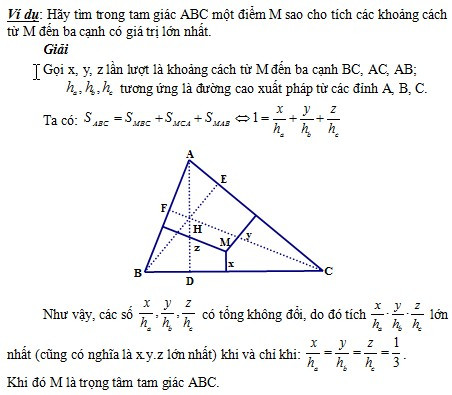 |
Theo thầy Mạnh Tường Vi, trong việc dạy và học, nhất là đối với môn Toán, việc tổ chức cho học sinh chủ động sáng tạo trong việc nắm bắt và vận dụng kiến thức là rất quan trọng. Sau đó việc hướng dẫn cho học sinh tự học, tự nghiên cứu là rất cần thiết.
Cho nên ở mỗi đơn vị kiến thức, nhất là đối với phần kiến thức mở, trước hết người dạy phải đầu tư thời gian tìm tòi nghiên cứu kiến thức, tìm phương pháp hướng dẫn cho học sinh học tập một cách tích cực chủ động, có như vậy thì việc dạy và học mới đạt hiệu quả cao, đồng thời rèn cho học sinh những phẩm chất của người lao động mới, năng động sáng tạo.
“Trong việc giảng dạy bộ môn Toán, tôi luôn hướng dẫn học sinh theo hướng: Mở rộng, tổng quát hoá, tìm hướng áp dụng kiến thức. Đặc biệt trong phần kiến thức về bất đẳng thức đại số, bất đẳng thức hình học ở lớp 8 và 9.
Xác định đây là phần kiến thức khó đối với học sinh, nhưng nó rất quan trọng trong việc rèn khả năng tư duy sáng tạo, phát triển khả năng tự học tự nghiên cưú cho học sinh. Tôi đã triển khai theo từng bước, đối với từng đối tượng học sinh” – Thầy Mạnh Tường Vi chia sẻ thêm.





































