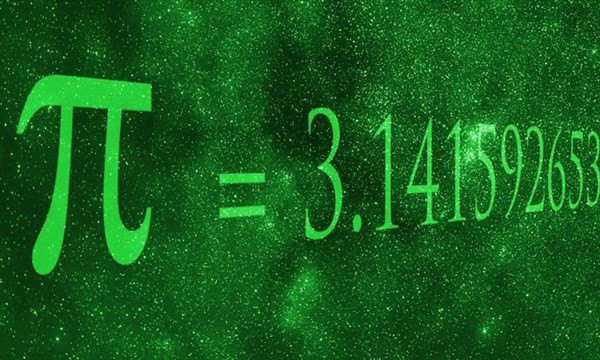Con số kéo dài vô tận
Số pi là một khái niệm cực kỳ dễ hiểu ngay cả với học sinh tiểu học. Nó đơn giản là tỷ lệ giữa chu vi và đường kính của một đường tròn. Hiển nhiên, với học sinh tiểu học hoặc trong các tính toán đơn giản không cần độ chính xác cao, người ta thường chỉ nhắc tới giá trị của nó là 3,13 hoặc chính xác hơn chút nữa là 3,1416.
Trên thực tế thì pi là một số vô tỷ, có nghĩa là nó không phải một tỷ số chính xác. Khi biểu diễn dưới dạng số thập phân thì nó là một số thập phân vô hạn không tuần hoàn, có nghĩa là số lượng chữ số ở phần thập phân của nó cứ kéo dài ra vô tận.
Tôi thì thường nhớ tới chữ số thập phân thứ 9, tức là 3,141592654, nhưng chắc chắn rằng nếu không được máy tính hỗ trợ mà cần tính nhẩm hay thậm chí là tính ra trên giấy những bài toán thông thường thì tôi không có đủ kiên nhẫn làm một phép tính với nhiều chữ số như vậy, vì nó chẳng để làm gì cả.
Vậy tại sao người ta cần tới rất nhiều chữ số của số pi và tại sao lại tồn tại một con số như vậy ở một nơi tưởng như vô cùng đơn giản là một đường tròn?
Độ dài của chu vi đường tròn
Một câu hỏi phát sinh khi nghĩ tới sự vô hạn của số pi là nếu như chu vi đường tròn bằng độ dài của đường kính nhân với pi thì phải chăng thực tế là chúng ta không bao giờ tính được chu vi chính xác của một đường tròn?
Câu trả lời là đúng như vậy. Trên thực tế, đường tròn là một khái niệm toán học. Nó không hề thực sự tồn tại. Không có bất cứ vật thể nào, hay thậm chí một hình mà bạn vẽ ra giấy bằng compa hay kể cả những công nghệ phức tạp nhất lại thực sự có dạng tròn tuyệt đối như toán học - tức khoảng cách từ tâm của nó tới bất cứ điểm nào trên đường tròn đều bằng nhau.
Hãy tưởng tượng rằng bạn xếp rất nhiều viên gạch lại thành một vòng tròn. Chẳng hạn đó là một vòng tròn có đường kính 20m. Nếu đứng ở tầng 10 của một tòa nhà và nhìn xuống vòng gạch bạn đã xếp trên mặt đất, bạn sẽ thấy nó là một đường tròn khá hoàn chỉnh. Nhưng khi xuống tới nơi, bạn vẫn nhận ra nó chỉ là tập hợp của những đoạn thẳng ngắn ghép lại (mỗi viên gạch là một đoạn đó).
Bạn có thể cầm một lon bia và thấy nó giống như một hình trụ khá hoàn hảo với bề mặt cong hoàn toàn trơn nhẵn. Nhưng thực tế, mọi việc không khác gì hàng gạch kia cả, chỉ khác ở chỗ các giác quan của bạn không đủ để cảm thấy sự có mặt của những “đoạn thẳng” rời rạc mà thôi.
Ở thang khoảng cách vi mô, bề mặt tưởng như trơn nhẵn đó cũng được hợp thành từ rất nhiều phân tử, và thậm chí những phân tử đó còn không giống nhau nên ở tháng đó thì thực tế là bề mặt của lon bia khá sần sùi.
Bây giờ, ngược lại, hãy giả sử ta chấp nhận rằng mặt cắt của lon bia là một đường tròn hoàn hảo, và có thể đo nó bằng cách dùng một chiếc thước dây quấn quanh một vòng, tỉ mỉ và cẩn thận. Hãy để ý điều này: Chiếc thước dây của bạn luôn có độ dày nhất định.
Nếu đó là một chiếc thước đủ dày, bạn sẽ thấy rõ rằng khi nó quấn quanh một thứ gì đó thì sự bẻ cong khiến cho mặt trong (mặt tiếp xúc với vật được quấn) bị dồn nén lại, khiến khoảng cách giữa các vạch chia không còn y như ban đầu. Với chiếc thước dây cực mỏng thì bạn không nhìn thấy rõ điều đó, nhưng nó vẫn cứ xảy ra.
Vì vậy, thực tế là bạn không bao giờ đo được chính xác tuyệt đối chu vi của một lon bia. Nói một cách rõ ràng hơn, đơn vị đo chiều dài chỉ có giá trị chính xác tuyệt đối khi áp dụng cho đường thẳng. Khi sử dụng nó vào việc đo đường cong, nó luôn có sai số.
Qua hai phân tích trên, bạn có thể thấy rằng, thực tế thì đường tròn, hay rộng hơn là đường cong nói chung, không bao giờ có giá trị chính xác về độ dài. Và thông qua số pi, chúng ta thấy được một cách trực quan nhất về tính thiếu chính xác đó.
Cần bao nhiêu chữ số cho pi?
Để dễ hình dung hơn về con số mà các nhà khoa học ở Thụy Sĩ đã tính ra, hãy làm phép tính thế này: Nếu bạn dùng giấy để viết hết 62,8 nghìn tỷ chữ số mà họ vừa tính ra thì giả sử mỗi trang giấy A4 có thể viết 2.000 chữ số, bạn sẽ cần tới hơn 30 tỷ trang giấy. Và nếu mỗi ngày bạn có thể viết tới 100 trang thì sẽ cần tới hơn 680 năm làm việc liên tục để làm điều đó.
Vậy chúng ta cần tới nó để làm gì? Thực tế thì chúng ta cần bao nhiêu chữ số cho pi?
Giả sử bạn cần xây một sân vận động có đường bao là đường tròn có đường kính 250m (tức là lớn hơn cả sân Camp Nou của Barcelona - sân vận động lớn nhất châu Âu), thì với việc lấy số pi từ chữ số thập phân thứ 5, thì sai số của chu vi đường tròn bao đó chỉ dao động khoảng 2mm. Với 9 chữ số thập phân như tôi nhớ được thì tôi có thể tính chu vi Trái đất với sai số không tới 2cm.
Ở thang vĩ mô hơn, theo thông tin từ Phòng Thí nghiệm sức đẩy phản lực (JPL) của NASA, họ chỉ cần tới số thập phân thứ 15 cho những tính toán về quỹ đạo của tàu không gian. Ở mức đó, một vòng tròn có đường kính 40 tỷ km - vượt ra rất xa khỏi quỹ đạo của sao Hải Vương và cả Pluto - được tính ra chu vi với sai số chỉ khoảng 1,5 inch (gần 4cm). Rõ ràng, sai số đó quá nhỏ để cần phải quan tâm.
Tới chữ số thập phân thứ 32, sai số khi tính chu vi của toàn bộ thiên hà Milky Way sẽ nhỏ hơn cả kích thước của một nguyên tử hydro.
Chúng ta hoàn toàn không cần tới 100 chữ số thập phân cho số pi làm gì cả. Vậy nhưng người ta vẫn cố tìm ra những thuật toán mới để mà đến nay đã tính ra hàng ngàn tỷ chữ số cho nó, và có những người dành thời gian để ghi nhớ thật nhiều chữ số của nó.
Có lẽ đơn giản là sự thách thức đối với chính các nhà toán học và chuyên gia về thuật toán cho máy tính, hoặc thú vui thích lập kỷ lục và khoe thành tích đặc biệt của mình.
Với đa số mọi người, những động cơ đó có vẻ phù phiếm và vô nghĩa. Nhưng chắc chắn, nhờ những người tiếp tục theo đuổi nó thì trong tương lai chúng ta sẽ còn nghe nhiều về việc tính toán con số này.