Chúng ta biết rằng, trên các diễn đàn nhiều giáo viên có đề cập đến soạn kế hoạch bài dạy mà trước đây người ta gọi là giáo án. Ai cũng biết, kế hoạch bài dạy là kịch bản của mỗi giáo viên; khi giáo viên đến lớp họ chuẩn bị bài dạy của mình với mong muốn truyền đạt kiến thức đến học sinh một cách tự nhiên mà không có sự gượng ép, nếu giáo viên có đầu tư và chuẩn bị chu đáo thì tiết dạy sẽ tốt.
Theo tôi, không nên “đồng phục” việc soạn kế hoạch bài dạy vì nó làm mất đi sự sáng tạo của giáo viên, miễn sao khi dạy giáo viên thể hiện rõ các cụm từ: Hoạt động khởi động, hoạt động hình thành kiến thức, hoạt động vận dụng là được. Là giáo viên lâu năm trong ngành tôi mạnh dạn đưa ra một quan điểm về cách soạn kế hoạch bài dạy của lớp 10 phân môn hình học để cùng trao đổi với quý đồng nghiệp như sau:
BÀI 3: GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TIỄN
Môn toán: Hình học. Lớp 10
Thời gian thực hiện:(số tiết: 02)
I. Mục tiêu
1. Kiến thức:
- Hiểu được giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
- Biết vận dụng giải tam giác vào thực tiễn dựa trên định lí côsin, định lí sin và các công thức diện tích vào bài toán giải tam giác.
- Biết phân biệt các dạng bài toán thực tế liên quan đến giải tam giác (loại tính độ dài hay tính chiều cao hoặc tính góc).
2. Năng lực:
- Năng lực tư duy và lập luận: Vận dụng được các công thức đã học liên quan đến các yếu tố trong tam giác để giải tam giác.
- Năng lực giải quyết vấn đề: Tiếp nhận câu hỏi và xử lý câu hỏi dựa trên các kiến thức liên quan đến các yếu tố trong tam giác.
- Năng lực giao tiếp: Biết trao đổi thông qua hoạt động nhóm nhưng phải biết lắng nghe, phản biện và chia sẻ.
- Năng lực mô hình hóa: Từ tư duy trực quan đến tư duy trừu tượng nghĩa là từ bài toán thực tiễn ta vận dụng kiến thức nào để giải quyết.
- Năng lực sử dụng công cụ và phương tiện học toán: Biết sử dụng máy tính cầm tay để tính toán và biết dùng thức để vẽ cạnh và góc.
3. Phẩm chất:
- Trách nhiệm: Học sinh có trách nhiệm với công việc được giao và chủ động hợp tác trong hoạt động nhóm.
- Thể hiện sự ham thích và chăm chỉ: Tự tìm được niềm vui trong học toán, từ đó vươn lên trong học tập. Tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức và biết cầu tiến trong học tập.
II. Thiết bị dạy học và học liệu
1. Đối với giáo viên: Thước thẳng có chia khoảng, compa, phiếu học tập, máy chiếu, sách giáo khoa, bài soạn.
2. Đối với học sinh: Dụng cụ học tập, sách giáo khoa, chuẩn bị bài trước khi đến lớp.
III. Phương pháp:
Vận dụng linh hoạt các PPDH nhằm giúp học sinh chủ động, tích cực trong phát hiện chiếm lĩnh tri thức, như: trình diễn, thuyết trình, giảng giải, gợi mở vấn đáp, nêu vấn đề. Trong đó phương pháp chính là: giảng giải, gợi mở vấn đáp và hoạt động nhóm.
IV. Tiến trình dạy học
1. Ổn định lớp: Kiểm tra sĩ số, chỗ ngồi học sinh.
2. Kiểm tra bài cũ:Yêu cầu học sinh lên bảng ghi lại nội dung định côsin và định lý sin trong tam giác.
3. Bài mới:
Hoạt động 1: Giới thiệu để vào bài mới
GV: Đặt câu hỏi 1. Cho tam giác giả sử ta biết cạnh cạnh và góc
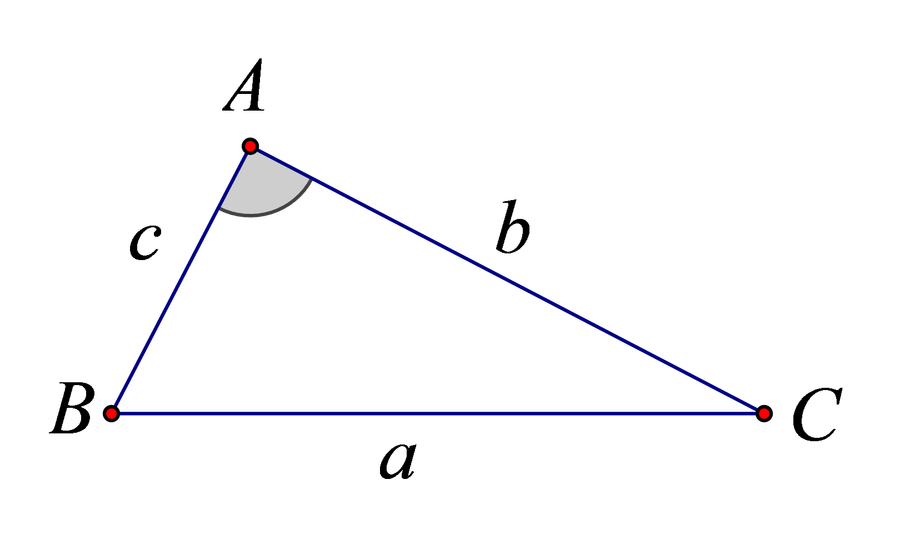 |
Khi đó, ta có tính cạnh và hai góc còn lại và được không ?
HS: Thảo luận trả lời là tính được.
Sản phẩm: Gọi là giải tam giác.
GV: Đặt câu hỏi 2.
 |
 |
+ Quan sát hình 1, liệu rằng ta có tính độ rộng của con sông mà không cần chèo thuyền ra đo được không ?
+ Quan sát hình 2, liệu rằng ta có tính độ cao của tòa nhà mà không trèo lên để đo được không ?
HS: Thảo luận và trả lời là đo được.
Sản phẩm: Áp dụnggiải tam giác vào thực tiễn.
GV: Vậy bài học hôm nay, chúng ta tìm hiểu giải tam giác và ứng dụng vào thực tiễn.
Hoạt động 2:Tiếp cận nội dung 1 của bài học: Giải tam giác.
1. GIẢI TAM GIÁC
GV: Giải thích Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết các yếu tố đủ để xác định tam giác đó.
Bài 1.Cho tam giác ABC, biết b = 16cm, c = 8cm, góc A = 60o. Hãy tính cạnh a và các góc B, góc C.
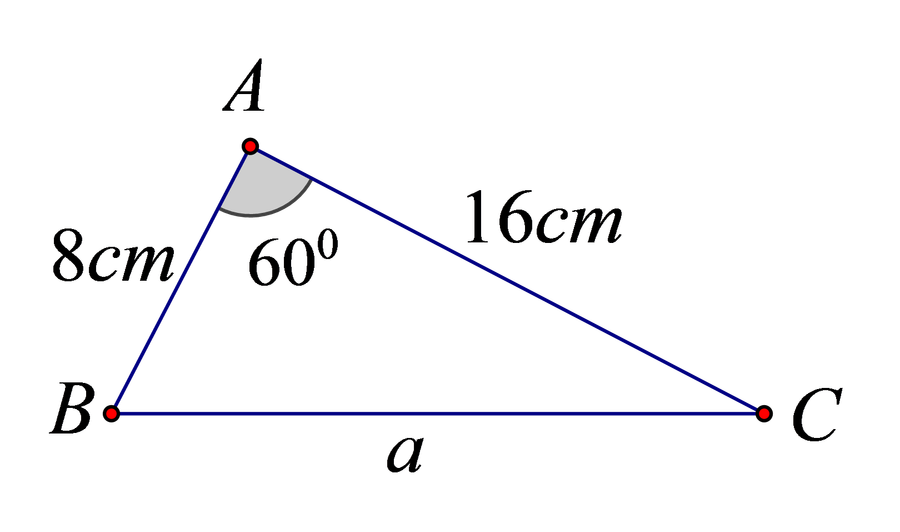 |
GV: Cho học sinh lên bảng vẽ hình.
HS: Một học sinh tự nguyện lên bảng vẽ hình.
Thảo luận nhóm để tính cạnh a và các góc B, góc C
GV: Cho học sinh lên bảng trình bày lời giải.
Sản phẩm: - Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.
- Kết quả: a = √192cm, góc B = 90o, góc C = 30o
Bài 2. (Trắc nghiệm) Cho tam giác ABC có góc A = 120o, góc B = 45o và cạnh b = 20cm
a) Số đo góc C bằng:
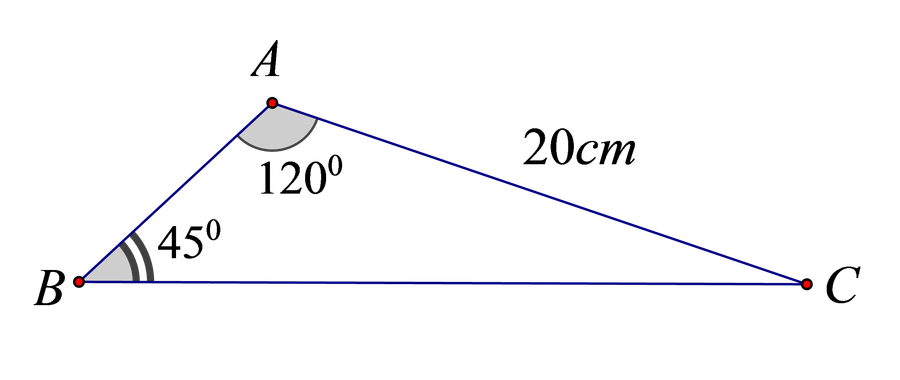 |
A. 15o B. 25o C. 5o D. 10o
GV: Cho học sinh suy nghĩ tìm lời giải.
HS: Thảo luận nhóm để tìm lời giải và chọn đáp án.
Sản phẩm: Kết quả đáp án A.
b) Độ dài bán kính R của đường tròn ngoại tiếp tam giác ABC bằng:
A. 10cm B. 10√3cm C. 10√2 D. 12cm
 |
GV: Cho học sinh suy nghĩ tìm lời giải.
HS: Thảo luận nhóm để tìm lời giải và chọn đáp án.
Sản phẩm: Kết quả đáp án C.
c) Độ dài cạnh AB (lấy một chữ số thập phân) bằng:
A. 15,2cm B. 15,5cm
C. 15,4cm D. 15,3cm
GV: Cho học sinh suy nghĩ tìm lời giải
HS: Thảo luận nhóm để tìm lời giải và chọn đáp án.
Sản phẩm: Kết quả đáp án D.
Hoạt động 3. Tiếp cận nội dung 2 là ứng dụng toán học vào thực tế.
GV: Dẫn dắt vào nội dung 2.
2. ỨNG DỤNG GIẢI TAM GIÁC VÀO THỰC TIỄN
GV: Giải thích vận dụng giải tam giác là giúp chúng ta giải rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Bài 3.(Ví dụ 2 SGK trang 75 của sách Chân trời sáng tạo)
Một đường hầm được dự kiến xây dựng xuyên qua một ngọn núi. Để ước tính chiều dài của đường hầm, một kĩ sư đã thực hiện các phép đo và cho ra kết quả như Hình 1. Tính chiều dài của đường hầm từ các số liệu đã khảo sát được.(làm tròn đến hàng đơn vị)
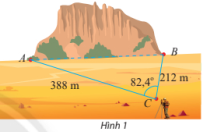 |
GV: Cho học sinh lên bảng trình bày lời giải.
(gợi ý dùng định lý côsin trong tam giác ABC)
HS:
- Thảo luận nhóm để tìm cách tính đoạn
- Một học sinh lên bảng trình bày lời giải.
Sản phẩm:
- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.
- Kết quả: AB ≈ 417m.
Bài 4.Một nhà khảo cổ học tìm được một phần của chiếc trống đồng có bề mặt trống là dạng hình tròn nhưng bị vỡ. Để xác định bán kính của chiếc trống, họ lấy ba điểm A, B, C trên vành trống, tiến hành đo đạc và thu được được số liệu BC = 28cm, góc BAC = 120o (Hình 2).
 |
Hãy tính bán kính R (lấy một chữ số thập phân) của chiếc trống.
GV: Cho học sinh lên bảng trình bày lời giải.
(gợi ý dùng định lý sin trong tam giác ABC)
HS:
- Thảo luận nhóm để tìm cách tính bán kính R.
- Một học sinh lên bảng trình bày lời giải.
Sản phẩm:
- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.
- Kết quả: R ≈ 16,2cm.
Bài 5. ( Ví dụ SGK trang 76của sách Chân trời sáng tạo)
Hai trạm quan sát ở hai thành phố Đà Nẵng và Nha Trang đồng thời nhìn thấy một vệ tinh với góc nâng lần lượt là 75o và 60o (Hình 3). Vệ tinh cách trạm quan sát tại thành phố Đà Nẵng bao nhiêu kilômét? (làm tròn đến hàng đơn vị). Biết rằng khoảng cách giữa hai trạm quan sát là 520km.
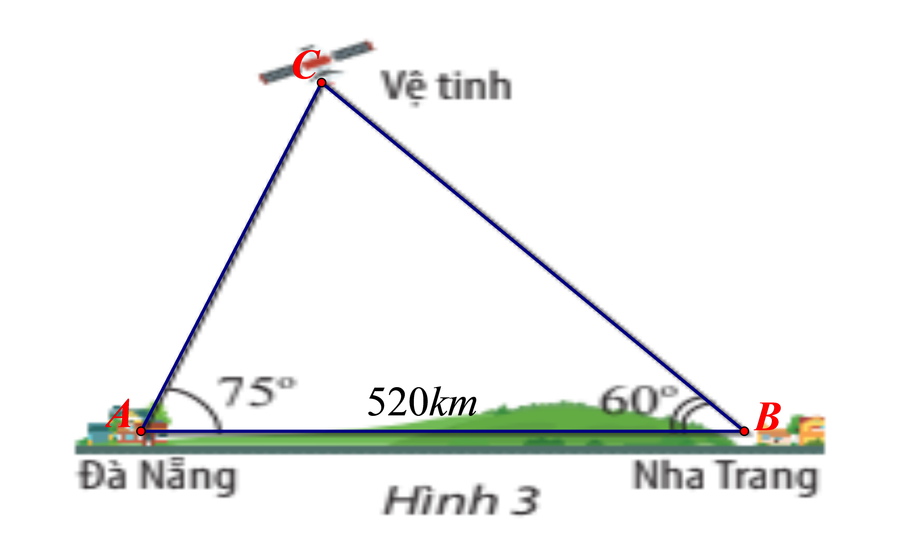 |
GV: Cho học sinh lên bảng trình bày lời giải.
(gợi ý dùng định lý sin trong tam giác ABC)
HS:
- Thảo luận nhóm để tìm cách tính đoạn AC.
- Một học sinh tự nguyện lên bảng trình bày lời giải.
Sản phẩm:
- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.
- Kết quả: góc C = 45o , AC ≈ 637km.
Bài 6. (Ví dụ 3 SGK trang 75 của sách Chân trời sáng tạo)
Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng RQA = 84o, người đó lùi ra xa một khoảng cách LM = 49,4m thì nhìn thấy đỉnh toà nhà với góc nâng RPA = 78o. Tính chiều cao của toà nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL. (Hình 2)
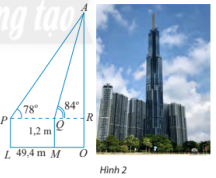 |
GV: Cho học sinh lên bảng trình bày lời giải.
(gợi ý dùng định lý sin trong tam giác ABC)
HS:
- Thảo luận nhóm để tìm cách tính đoạn AO.
- Một học sinh lên bảng trình bày lời giải.
Sản phẩm:
- Nhận xét cách trình, giải thích đúng sai và cho học sinh
ghi lời giải vào vở.
- Kết quả: góc PAQ = C, AR ≈ 460m, AO = 460 + 1,2 = 461,2m.
Bài 7. (Bài 7 SGK trang 77 của sách Cánh diều)
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Phương nghiêng của góc quan sát từ vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45o và 75o .Biết khoảng cách giữa hai vị trí A và B là 30m (Hình 4). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn đến hàng đơn vị).
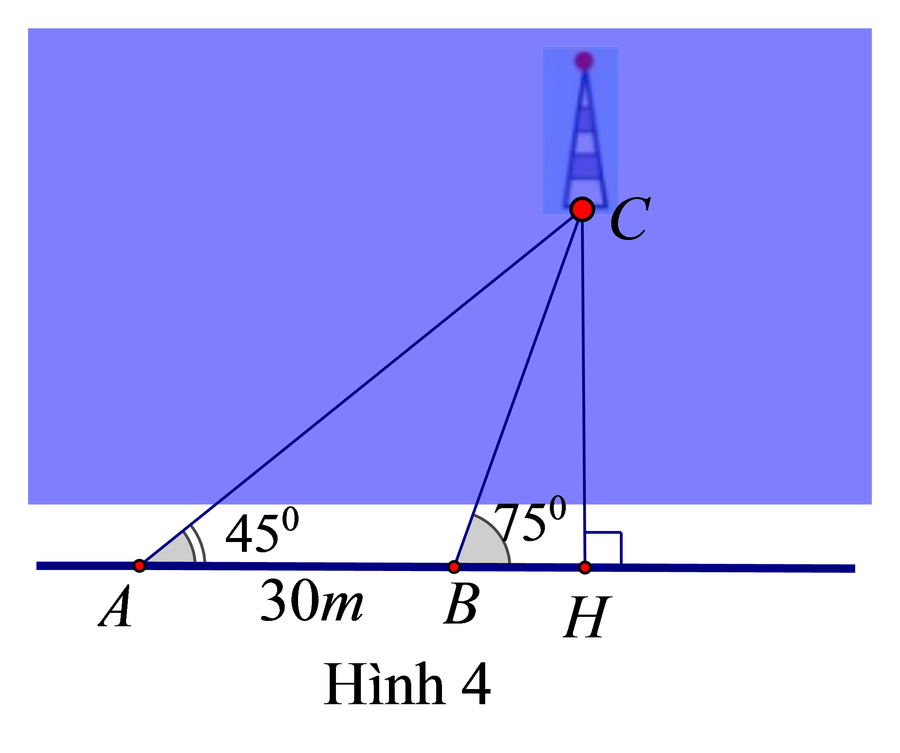 |
GV: Cho học sinh lên bảng trình bày lời giải.
(gợi ý dùng định lý sin trong tam giác ABC)
HS:
- Thảo luận nhóm để tìm cách tính đoạn CH
- Một học sinh tự nguyện lên bảng trình bày lời giải.
Sản phẩm:
- Nhận xét cách trình, giải thích đúng sai và cho học
sinh ghi lời giải vào vở.
- Kết quả: góc ABC = 105o, góc ACB = 30o
BD = 30.sin45o/sin30o ≈ 42m, CH = BDsin75o ≈ 41m
4. Củng cố: Giáo viên nhắc lại cho học sinh hiểu giải tam giác và ứng dụng toán học vào thực tế.
5. Hướng dẫn về nhà:
CHUYỂN GIAO NHIỆM VỤ
Phần 1. Trắc nghiệm
Câu 1. Cho tam giác ABC với BC = 5cm, CA = 4cm, AB = 3cm. Khi đó, diện tích tam giác ABC bằng:
A. 12cm2 B. 6cm2 C. 15cm2 D. 10cm2
Câu 2. Cho tam giác có diện tích S = 10cm2 và cạnh a = 4cm. Khi đó, đường cao h của tam giác ABC bằng:
A. 20cm B. 4cm C. 5cm D. 10cm
Câu 3. Cho tam giác ABC với BC = a, CA = b, AB = c. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Hãy chọn khẳng định đúng trong các khẳng định sau:
A. a = 3RsinA B. R = a/3sinA C. c = RsinC D. b = 2RsinB
Câu 4. Cho tam giác ABC, với góc A = 30o, CA = 4cm, AB = 3cm. Khi đó, cạnh BC bằng:
A. 37cm B. √37cm C.13cm D.√13cm
Câu 5. Cho tam giác ABC với góc A = 30o, BC = 3cm Khi đó, bán kính R của đường tròn ngoại tiếp tam giác ABC bằng:
A. 4cm B. 3cm C. 6cm D. 3/2cm
Câu 6. Hai chiếc tàu cùng xuất phát từ một địa điểm A. Sau 3 giờ, tàu thứ nhất đã đến địa điểm B với quãng đường 130M (130 Hải lý) và tàu thứ hai đã đến địa điểm C với quãng đường 80M (80 Hải lý), biết hướng đi của hai tàu luôn hợp với nhau một góc bằng 120o (tham khảo hình vẽ dưới).
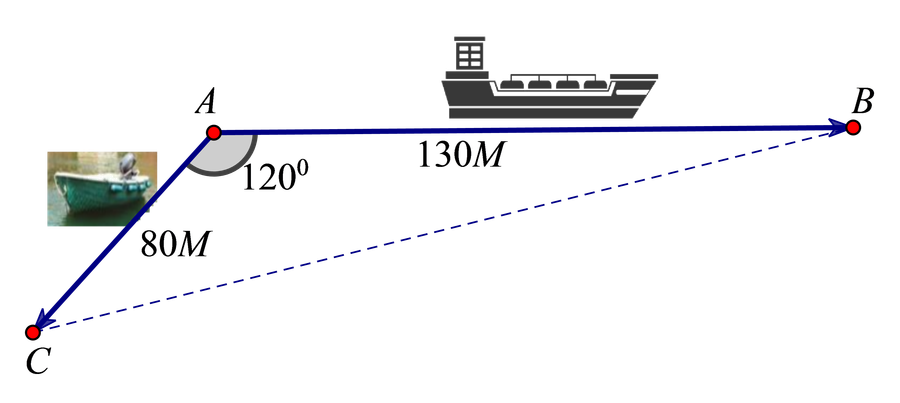 |
Khi đó, hai tàu cách nhau bao nhiêu hải lý ?
A. 10√209M B. 33700M C. 20900M D. 10√337M
Câu 7. Cho tam giác ABC có diện tích S = 8√2 và nửa chu vi P = 4. Khi đó, bán kính R của đường tròn nội tiếp tam giác ABC bằng:
A. √2 B. 4√2 C. 2√2 D. 2
Câu 8. Một nhà khảo cổ học tìm được một chiếc cổ hình tròn nhưng bị vỡ. Để xác định bán kính của chiếc đĩa, họ lấy ba điểm A, B, C trên vành đĩa, tiến hành đo đạc và thu được được số liệu BC = 30cm, góc BAC = 120o (tham khảo hình vẽ dưới).
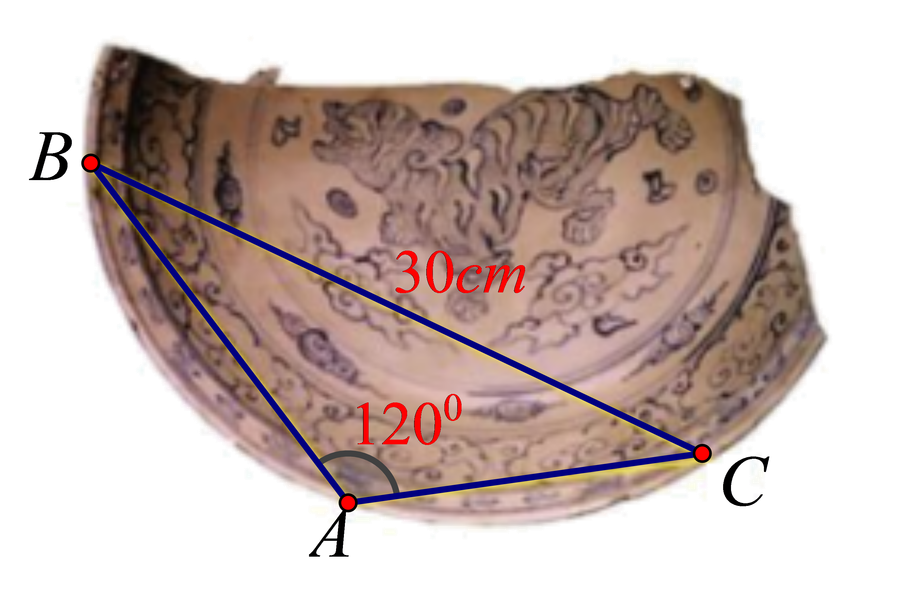 |
Khi đó, bán kính R (lấy một chữ số thập phân) của chiếc đĩa bằng:
A. 16,4cm B. 17,3cm C. 17,8cm D. 18,3cm
Câu 9. Cho tam giác ABC với BC = a, CA =b, AB= c.Hãy chọn khẳng định sai trong các khẳng định sau:
A. cosC = a2 + b2 - c2/2ab B. cosA = b2 + c2 - a2/2bc
C. cosB = a2 + c2 - b2/2ac D. cosB = a2 + c2 + b2/2ac
Câu 10. Bạn Minh đứng ở vị trí A trên bờ biển để nhìn ra vị trí C của hòn đảo với góc nghiêng là 30o so với bờ biển. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng bằng 100m và cũng nhìn về vị trí C với góc nghiêng là 40o so với bờ biển (tham khảo hình vẽ dưới).
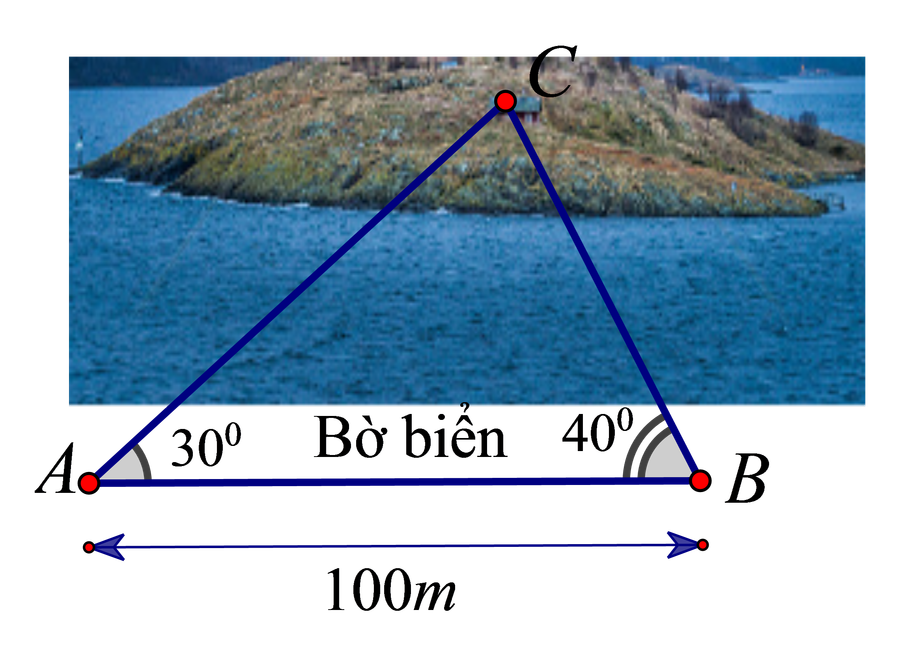 |
Khi đó, độ dài đoạn AC (lấy một chữ số thập phân) bằng:
A. 72,6cm B. 58,6cm C. 78,4cm D. 68,4cm
Đáp án
| 1.B | 2.C | 3.D | 4.D | 5.B |
| 6.D | 7.C | 8.B | 9.D | 10.D |
Phần 2. Tự luận: Giáo viên yêu cầu học sinh làm bài tập trong sách giáo khoa.