Dẫn dắt để học sinh từ tìm tri thức
Trong thời gian giảng dạy, thầy Hà Ngọc Long cho biết, bản thân luôn nghiên cứu, tìm tòi các phương pháp mới phù hợp với từng bài dạy và đối tượng học sinh để truyền thụ kiến thức, đặc biệt trong việc dạy học các định lý.
Cụ thể: Luôn đưa ra kiến thức một cách tự nhiên, bằng cách dẫn dắt từng bước cho học sinh tự tìm lấy; phân tích hướng dẫn học sinh thấy ý nghĩa, ứng dụng của định lý; sau đó đưa ra hệ thống bài tập áp dụng tương thích.
Với phương pháp truyền thụ như trên, học sinh hứng thú và nhớ lâu kiến thức, đồng thời vận dụng tốt trong quá trình giải và khai thác các bài tập.
Trong số các định lý đã truyền đạt cho học sinh, thầy Long cho biết đặc biệt chú ý đến phần Định lý Cosin trong tam giác.
Với thời lượng nửa tiết học chính khóa, học sinh chỉ có thể hiểu được nội dung, hệ quả định lý và áp dụng vào giải quyết một vài bài toán cơ bản trong tam giác.
Tuy nhiên, việc giới thiệu và chứng minh định lý thế nào để tất cả học sinh hiểu là không hề đơn giản.
Áp dụng cụ thể với tìm hiểu định lý Cosin
Theo thầy Hà Ngọc Long, khi trình bày chuyên đề Định lý Cosin và ứng dụng, giáo viên cần làm rõ 2 nội dung: Giới thiệu định lý, dẫn dắt học sinh chứng minh định lý, phát hiện các hệ quả, ý nghĩa của định lý; đồng thời hệ thống các bài toán giúp học sinh biết cách khai thác ứng dụng của định lý.
Dưới đây là những chia sẻ của thầy Long giúp học sinh nắm vững lý thuyết và phương pháp giải cho từng dạng Toán.
Nội dung 1: Hướng dẫn học sinh tìm hiểu nội dung, ý nghĩa của định lý Cosin trong tam giác:
Tam giác hoàn toàn xác định khi biết 3 cạnh, hoặc hai cạnh và một góc xen giữa, hoặc biết một cạnh và hai góc kề. Các góc cạnh còn lại và góc cạnh đã biết sẽ có một mối liên hệ. Các mối liên hệ đó người ta gọi là các hệ thức lượng giác trong tam giác. Một trong các hệ thức đó là Định lý Cosin trong tam giác.
 |
Giáo viên có thể đưa ra một số lưu ý để học sinh ghi nhớ được nội dung định lý
Thông qua cách trình bày trên, học sinh hoàn toàn phát hiện và nêu được các ý nghĩa của định lý:
1. Để xác định được 1cạnh của tam giác thì cần biết hai cạnh khác và 1 góc xen giữa ( Học sinh phân biệt được với định lý sin sau này)
2. Hệ quả: Từ định lý học sinh rút ra được:
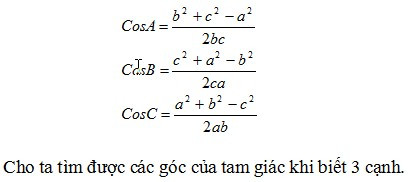 |
3. Cho phép ta xét được các góc trong tam giác là nhọn, tù hay vuông thông qua các yếu tố cạnh của tam giác.
 |
4. Xây dựng công thức tính độ dài đường trung tuyến trong tam giác:
 |
5. Liên hệ với diện tích trong tam giác:
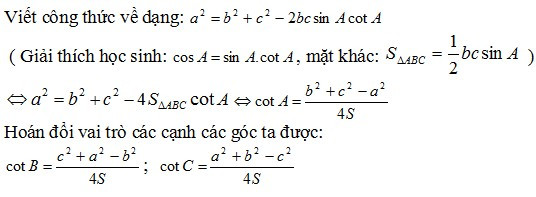 |
Đây là định lý “Cosin suy rộng trong tam giác”, cho ta hệ thức lượng giác về mối liên hệ giữa các góc của tam giác với 3 cạnh cùng diện tích của nó. Lớp các bài toán áp dụng nó khá rộng.
6. Ngoài ra sử dụng định lý, hệ quả kết hợp các kiến thức khác giải quyết các bài toán về hệ thức lượng trong tam giác, nhận dạng tam giác, …
Nội dung 2: Cách thức khai thác định lý Cô sin vào giải một số bài toán:
Từ các ý nghĩa, tác dụng của định lý giáo viên có thể hướng dẫn học sinh giải quyết các bài toán liên quan tương thích như sau:
 |
Tuy nhiên với phương pháp này, thầy Long lưu ý, giáo viên phải biết vận dụng sáng tạo phương pháp phù hợp với kiến thức đang cần truyền thụ cho học sinh; đánh giá đúng đối tượng học sinh để giới thiệu và khai thác kiến thức một cách phù hợp.





































